The story in the heterotic theory is more interesting and inspiring. The type I Yang-Mills supergravity theory in ten-dimensions is the low energy effective limit of the type I superstring theory and the heterotic string theory. String theories require higher order corrections to their corresponding low energy supergravity effective actions. The leading type II string corrections are of order, and include terms (the fourth power of the Riemann tensor), both at tree level and one loop. These corrections are also present in the type I/heterotic effective actions and in M-theory. These string corrections to supergravity theories should obviously be supersymmetric. Unfortunately there is still no known way to compute these corrections in a manifestly supersymmetric way, although important progresses have been achieved. The supersymmetrization of these higher order string/M-theory terms has been a topic of research for a long time. In this situation, one might try to study the constraints that ten-dimensional supersymmetry imposes on higher-order contributions to the effective action. One difficulty here is that, with the exception of the supergravity sector of the heterotic string, it is not known how to construct any superspace actions due to the absence of any known sets of auxiliary fields. Even in the heterotic case, the auxiliary fields are rather complicated and it is not clear how to construct higher order actions which correspond to superstring corrections, although the invariant was discussed from this point of view. Although supergravity theory was not shown to be a finite perturbation theory to all orders, their effective actions are still crucial for many applications, especially because of the remarkable fact that they turned out to describe the low-energy effective behavior of superstring theories. Several different methods can be use to formulate supergravity theories and their derivative corrections. This mechanism of calculating the low-energy effective action might be applied as well for supersymmetric string, i.e. superstring theory. Indeed, it has been shown that the low-energy approximation of superstring is the 10-dimensional supergravity, locally supersymmetric quantum field theory. We will introduce the supergravity action as the low-energy effective action of superstring theories. We shall also outline various approaches that have been used to construct such an action and the corresponding higher derivative corrections. Field redefinitions and equivalent effective actions will be studied for the heterotic string to the order, having the Chern-Simons terms included. We have devoted this article to introduce a supergravity action as the low-energy effective action of a superstring theory, outlining the most powerful methods that have been pursued for constructing such an action and the contributions to them. We will begin with the ten-dimensional spacetime Lagrangian of the anomaly-free heterotic supergravity coupled to Yang-Mills fields. In the supergravity literature, this is often referred to as the nonmaximal ten-dimensional supergravity, in order to distinguish it from the N=2 supergravities with 32 supercharges. The relevant Lagrangian was constructed in several steps, starting with the four-dimensional, N=4 supergravity multiplet covariantly coupled to an abelian (Maxwell) multiplet. This Lagrangian can be straightforwardly interpreted as the dimensional reduction of a ten-dimensional N=1 supergravity theory coupled to an abelian gauge field. Extension to a sector with nonabelian Yang-Mills fields requires inclusion of a crucial Kalb-Ramond term in the Lagrangian, necessitated by the mixed gauge-gravity anomaly cancellation conditions. Another feature of interest in this Lagrangian is the possibility of a field-dualization: the Lagrangian can be expressed interchangeably in terms of either a two-form, or a six-form, supergravity potential. The former choice is natural from the perspective of the string supergravities: the low-energy spacetime effective action of the heterotic string theory has a Neveu-Schwarz sector two-form potential, that can couple to the fundamental closed string. The standard procedure for producing a lower-dimensional supergravity from a higher-dimensional one is to propose a reduction ansatz for the higher-dimensional fields, which is substituted into the higher-dimensional action. One then integrates out all internal coordinate dependence in the higher-dimensional action. By contrast, a dimensional reduction is simply an algorithm that may be employed to obtain a lower-dimensional supergravity from a higher-dimensional one. In order to perform a dimensional reduction of a supergravity, we need to know what forms to expand the ten-dimensional fields. For the lower dimensional theories one may consider the dimensional reduction of the D = 10 Abelian Yang-Mills supergravity which is the maximal torus subtheory of the D = 10 Yang-Mills supergravity. The scenario of dimensional reduction provides us with a setting in which an effective four dimensional theory can be obtained from the ten dimensional supergravity theories, therefore bringing four dimensional physics in contact with string theory. Their possible stringy origin, as higher order terms in string/M theory after compactification from ten/eleven dimensions, is often neglected. One of the reasons for that criterion is chronological: the study of the quantum properties of four dimensional supergravity theories started several years before superstring theories were found to be free of anomalies and taken as the main candidates to a unified theory of all the interactions. In higher dimensions the procedure has been different: the low-energy limits of superstring theories are the different ten-dimensional supergravity theories. People have studied higher order corrections to these theories most of the times in the context of string theory, which requires them to be supersymmetric. We provide a detailed study of the phenomenology of compactifications of the heterotic string within the context of supergravity effective theories. The structure of heterotic string theory rests upon the fact that closed strings which form this theory have independent the right and left moving sectors. In heterotic string, one sector is supersymmetric, namely the theory has N = 1 supersymmetry. This can be seen from the fact that the left moving sector can coincide with a purely bosonic strings, contrasting with a right moving sector which consists of modes of a superstring. In heterotic string theory we do have a non-abelian gauge theory which results from the compactification of the bosonic sector on a 16-dimensional compact internal space, yielding 10-dimensional superstring theory. Note that it is very natural in heterotic supergravity to include the first order corrections, since at zeroth order the gauge field decouples, and one loses some of the massless modes of the corresponding string theory. On the other hand, it is not entirely clear that a supergravity solution can be lifted to a full string background, since solutions to the first order equations often depend explicitly on the corrections, and higher order corrections potentially become large. All our analysis is performed at the supergravity level using an effective field theory approach. Several simplifying assumptions are made, in order to restrict the theory to a tractable system.
Heterotic Supergravity
The field theory limit of the heterotic string is given by ten-dimensional N=1 supergravity coupled to N=1 supersymmetric Yang–Mills. This theory was constructed generalising the construction for the abelian theory. The ten-dimensional heterotic supergravity contains the vielbein, the NS-NS two-form field, the dilaton, the anti-hermitian gauge field, as bosonic fields, and the gravitino, the dilatino and the gaugino. To set our field conventions, we give here the string frame action of the effective supergravity for the bosonic fields and gaugino
where
The string-frame supersymmetric variations of the dilatino, gaugino, and gravitino are
The Lagrangian, up to quartic fermion terms, is given by
where
where the field strengths are defined as
The supersymmetry transformations, up to terms cubic in fermion, are
The corresponding ten-dimensional Lagrangian, in the Einstein frame, can be written as
The bosonic sector of the Lagrangian clearly involves the Einstein-Hilbert action in ten dimensions, the kinetic term for the higher-dimensional dilaton, the kinetic term for the gauge fields and the corresponding one for the three-form. The three-form is sourced by the B-field plus additional corrections from Chern-Simons forms related to the cancelation of anomalies. In the fermionic part of the Lagrangian, appear all the kinetic terms for the fermion fields: gravitino, dilatino and gaugino. Finally the Lagrangian contains the interactions among the various fields of the theory.
The new string-frame action is
We find the linearized equations of motion for the gaugino, dilatino and gravitino
After some simplification, the string-frame action is
Using the relations above, and the fact that the product of more than three gamma matrices with all holomorphic or antiholomorphic indices is zero, we have
Similarly
and
The fields of the heterotic supergravity coupled to super Yang-Mills, which is the low-energy limit of the heterotic superstring theory, consist of the N = 1, D = 10 supergravity multiplet which contains the fields: the graviton, the gravitino which is a Rarita-Schwinger field, the two-form potential, the dilatino which is a Majorana-Weyl spinor, and the dilaton which is a scalar, coupled to an N = 1, D = 10 vector supermultiplet which contains the gauge field and the corresponding gaugino.
The heterotic supergravity with higher-order corrections has been well investigated. Let us write down the Lagrangian of ten-dimensional heterotic supergravity, which is an extended versions of the heterotic theory with higher-order corrections
where the Lagrangians are
We define the derivative on fundamental fields as
Let us show the local supersymmetry variations
It is both useful and instructive to obtain the supersymmetry algebra. The commutator of two supersymmetry variations reads
Expressed in terms of the Einstein frame metric, and to lowest order in the inverse string tension, the total Lagrangian takes the form
Notice the Chern-Simons contribution to the three-form field strength. Hats on the curvatures denote the supercovariant derivatives. Explicitly, we have
Thus, we will require that all spinor fields gravitino, dilatino, and gaugino, also transform in the adjoint representation of the large N flavor group. Keeping only the terms in previous Lagrangian that remain after planar reduction, gives the following supermatrix Lagrangian
Suppressing the dependence, we obtain the matrix Lagrangian
Scherk–Schwarz Dimensional Reduction
Scherk-Schwarz reductions are a generalization of Kaluza-Klein reductions in which the higher dimensional fields are allowed to have a dependence on the compactified coordinates. This is possible only if the higher dimensional theory has a global symmetry and the dependence is dictated by this symmetry. In the present section, we demonstrate how the preceding conjecture is realized for generalized toroidal compactifications of heterotic string theory. In this case, the standard Kaluza-Klein reduction on a d-dimensional torus from 10 to 10−d dimensions produces a theory with global O(d,d + 16) symmetry. The effective action can be organized to make the former U-duality symmetry manifest. We will show that this global symmetry is retained in the massive theories produced by generalized Scherk-Schwarz reductions. The bosonic part of effective action may be written as
where the scalar potential takes the simple form
The essential point is that the various mass parameters introduced by the generalized reduction can be organized as a completely antisymmetric three-index tensor under the O(d,d + 16) transformations. These parameters play a dual role in the reduced theory: first, as mass parameters defining the scalar potential potcovariant, and second as structure constants in the non-abelian gauge group of this theory. That is the generalized reduction has produced a gauged supergravity with a nontrivial non-abelian symmetry.
We begin with a review of the standard Kaluza-Klein reduction of low energy heterotic string theory on a d-torus. Our notation will be such that d + D = 10 and hence this compactification yields an effective D-dimensional theory. In ten dimensions, the low energy action is
The ten-dimensional fields are the dilaton, string-frame metric, Ricci scalar, Kalb-Ramond three-form field strength, and the Yang-Mills field strengths. The reduced action in D dimensions may be decomposed as follows
where the reduced metric-dilaton-two-form action is
the scalar moduli action is
and the gauge field action is
We continue with the metric-dilaton sector, which is given by
We can expand the ten-dimensional Ricci scalar and dilaton in terms of fields in the D-dimensional space-time. The previous action becomes
where we have used the following definitions
We can now reduce the Yang-Mills sector. The ten-dimensional action is
we arrive at
where we use
which again follow straightforwardly by dimensional reduction. The last contribution to the action comes from the three-form kinetic terms in ten dimensions
The reduction of this action produces the following action in D dimensions
The reduced three-form field strength is
With this, we finally find the reduced Kalb-Ramond action in D dimensions
The general massive reductions produce reduced theories with a remarkably symmetric form, where a part of the O(d, d+16) duality must be gauged in order to accommodate the couplings induced by the mass terms. Here, we are lead to a slight puzzle. Quantization conditions seem to break the O(d, d + 16,R) symmetry of the reduced action to O(d, d + 16,Z). Another aspect of the reduced theory was that a part of the global O(d, d + 16,R) symmetry becomes a local gauge symmetry. Thus it would seem that this continuous subgroup of the U-duality group must also be exact since it corresponds to a constant gauge transformations. The puzzle is to understand the interplay of these two apparent exact symmetries.
where
The string-frame supersymmetric variations of the dilatino, gaugino, and gravitino are
The Lagrangian, up to quartic fermion terms, is given by
where
where the field strengths are defined as
The supersymmetry transformations, up to terms cubic in fermion, are
The corresponding ten-dimensional Lagrangian, in the Einstein frame, can be written as
The bosonic sector of the Lagrangian clearly involves the Einstein-Hilbert action in ten dimensions, the kinetic term for the higher-dimensional dilaton, the kinetic term for the gauge fields and the corresponding one for the three-form. The three-form is sourced by the B-field plus additional corrections from Chern-Simons forms related to the cancelation of anomalies. In the fermionic part of the Lagrangian, appear all the kinetic terms for the fermion fields: gravitino, dilatino and gaugino. Finally the Lagrangian contains the interactions among the various fields of the theory.
The new string-frame action is
We find the linearized equations of motion for the gaugino, dilatino and gravitino
After some simplification, the string-frame action is
Using the relations above, and the fact that the product of more than three gamma matrices with all holomorphic or antiholomorphic indices is zero, we have
Similarly
and
The fields of the heterotic supergravity coupled to super Yang-Mills, which is the low-energy limit of the heterotic superstring theory, consist of the N = 1, D = 10 supergravity multiplet which contains the fields: the graviton, the gravitino which is a Rarita-Schwinger field, the two-form potential, the dilatino which is a Majorana-Weyl spinor, and the dilaton which is a scalar, coupled to an N = 1, D = 10 vector supermultiplet which contains the gauge field and the corresponding gaugino.
The heterotic supergravity with higher-order corrections has been well investigated. Let us write down the Lagrangian of ten-dimensional heterotic supergravity, which is an extended versions of the heterotic theory with higher-order corrections
where the Lagrangians are
We define the derivative on fundamental fields as
Let us show the local supersymmetry variations
Note that various objects such as a spin connection modified by the H-flux, supercovariantizations, and so forth
We also pick up the supercovariant derivatives at hand
It is both useful and instructive to obtain the supersymmetry algebra. The commutator of two supersymmetry variations reads
Expressed in terms of the Einstein frame metric, and to lowest order in the inverse string tension, the total Lagrangian takes the form
Notice the Chern-Simons contribution to the three-form field strength. Hats on the curvatures denote the supercovariant derivatives. Explicitly, we have
Thus, we will require that all spinor fields gravitino, dilatino, and gaugino, also transform in the adjoint representation of the large N flavor group. Keeping only the terms in previous Lagrangian that remain after planar reduction, gives the following supermatrix Lagrangian
Suppressing the dependence, we obtain the matrix Lagrangian
Scherk–Schwarz Dimensional Reduction
Scherk-Schwarz reductions are a generalization of Kaluza-Klein reductions in which the higher dimensional fields are allowed to have a dependence on the compactified coordinates. This is possible only if the higher dimensional theory has a global symmetry and the dependence is dictated by this symmetry. In the present section, we demonstrate how the preceding conjecture is realized for generalized toroidal compactifications of heterotic string theory. In this case, the standard Kaluza-Klein reduction on a d-dimensional torus from 10 to 10−d dimensions produces a theory with global O(d,d + 16) symmetry. The effective action can be organized to make the former U-duality symmetry manifest. We will show that this global symmetry is retained in the massive theories produced by generalized Scherk-Schwarz reductions. The bosonic part of effective action may be written as
where the scalar potential takes the simple form
The essential point is that the various mass parameters introduced by the generalized reduction can be organized as a completely antisymmetric three-index tensor under the O(d,d + 16) transformations. These parameters play a dual role in the reduced theory: first, as mass parameters defining the scalar potential potcovariant, and second as structure constants in the non-abelian gauge group of this theory. That is the generalized reduction has produced a gauged supergravity with a nontrivial non-abelian symmetry.
We begin with a review of the standard Kaluza-Klein reduction of low energy heterotic string theory on a d-torus. Our notation will be such that d + D = 10 and hence this compactification yields an effective D-dimensional theory. In ten dimensions, the low energy action is
The ten-dimensional fields are the dilaton, string-frame metric, Ricci scalar, Kalb-Ramond three-form field strength, and the Yang-Mills field strengths. The reduced action in D dimensions may be decomposed as follows
where the reduced metric-dilaton-two-form action is
the scalar moduli action is
and the gauge field action is
We continue with the metric-dilaton sector, which is given by
We can expand the ten-dimensional Ricci scalar and dilaton in terms of fields in the D-dimensional space-time. The previous action becomes
where we have used the following definitions
We can now reduce the Yang-Mills sector. The ten-dimensional action is
we arrive at
where we use
which again follow straightforwardly by dimensional reduction. The last contribution to the action comes from the three-form kinetic terms in ten dimensions
The reduction of this action produces the following action in D dimensions
The reduced three-form field strength is
With this, we finally find the reduced Kalb-Ramond action in D dimensions
The general massive reductions produce reduced theories with a remarkably symmetric form, where a part of the O(d, d+16) duality must be gauged in order to accommodate the couplings induced by the mass terms. Here, we are lead to a slight puzzle. Quantization conditions seem to break the O(d, d + 16,R) symmetry of the reduced action to O(d, d + 16,Z). Another aspect of the reduced theory was that a part of the global O(d, d + 16,R) symmetry becomes a local gauge symmetry. Thus it would seem that this continuous subgroup of the U-duality group must also be exact since it corresponds to a constant gauge transformations. The puzzle is to understand the interplay of these two apparent exact symmetries.
Heterotic M-theory
Heterotic M-theory is based on the idea that one of the low-energy limits of M-theory can be formulated as 11-dimensional supergravity with matter fields living on two halves of a 10-dimensional boundary. Recently Hořava and Witten proposed that the strong coupling limit of heterotic string theory can be described by 11-dimensional supergravity on a manifold with boundary where the two gauge multiplets are restricted to the two 10-dimensional boundaries respectively. Now that we have explained one way in which dynamical gauge fields on the boundary can be related to the topological gauge theory of the gauge field in the interior we will indicate how it can be compatible with the outstanding example of M-theory on a manifold with spatial boundary, namely the Hořava-Witten model of heterotic M-theory. We shall construct the Lagrangians and boundary conditions for the theory, mostly by direct reduction from 11 dimensions, resorting to supersymmetry only when the technical complexity becomes too daunting. It is precisely here that our effective supergravity Lagrangian, as derived from M-theory, adds important new information. It is interesting to consult the supersymmetry variations for the bulk fields. In heterotic M-theory, the incorporation of E8 super Yang-Mills theories on the two orbifold fixedplanes, simultaneously requires the augmentation of the susy-variations of the bulk-fields. The only non-vanishing contributions for constant Majorana-spinor derive from the boundary fields
The construction of Hořava-Witten supergravity proceeds by a power series in the expansion parameter. To lowest order, one starts with the action of N=1, D=11 supergravity
The covariant derivative of the gravitino, the spin connection and the 4-form field strength are defined as
Altogether the D=10 boundary action for the vector supermultiplet, comprising the gauge field and the gaugino, coupled to the bulk supergravity in a locally supersymmetric fashion, reads
From the field-theoretic point of view, we have to look for small fluctuations of the bulk fields in order to mediate interactions between the boundary fields. This will be achieved by using the background field method, according to which we split the bulk fields into a fixed classical background and the quantum fields, which propagate on this background. The action is then expanded around the background fields into a power series of the quantum fields.
In the expansion around the classical background, the bulk field fluctuations come equipped with an additional power. Summarizing, a consistent truncation implies throwing away all bulk-boundary interactions of order or higher. Thus, the remaining interaction terms are given by
We concentrate merely on the 3-vertices, the relevant couplings are
Since every term comprises exactly two boundary fields, it is convenient for the later comparison with the string amplitudes to rescale the super Yang-Mills fields which bear mass dimensions to
The fields have D-dimensional mass dimensions for D=10. This rescaling gives a canonical factor for the interaction terms, which eventually read
We begin with some of the ingredients of the improved version of low-energy heterotic M-theory. The theory is formulated on a manifold with a boundary consisting of two disconnected components with identical topology. The supergravity multiplet is placed on the manifold and Yang-Mills multiplets live on the boundary. Branes may be present, but we leave these out in the simplest version of the theory. The eleven-dimensional part of the action is conventional for supergravity
The boundary terms which make the action supersymmetric are
There are also boundary terms with the Yang-Mills multiplets. These are scaled, by a parameter, compared to the supergravity terms
The contribution to the action from the bulk is given by
The five-dimensional Lagrangian was obtained by a combination of the reduction ansatz for the bosonic terms and then by a comparison with the known five-dimensional supergravity models.
The first surface terms we consider are ones obtained from a reduction of the the supergravity boundary terms
The Lagrangians are
The remaining surface terms contain the matter fields and their couplings to the bulk supergravity fields
The Lagrangian for the Yang-Mills multiplet is
There are also new curvature-squared terms in the boundary action, which we obtain from the Yang-Mills terms
The supersymmetry of the full action with the new boundary terms follows from the gravity-Yang-Mills calculation. The modified curvature has been used for consistency between the derivative orders of the bosonic and fermionic terms. Variations of the new boundary term with the tetrad can be decomposed into metric variations and local Lorenz rotations
The bulk Lagrangian for the reduction of heterotic M-theory, when truncated at the fermion bilinear terms, is given by
The matter Lagrangian on the boundary is
On the boundary
The supersymmetry transformations of the fields on the boundary become
The total action followed by an account of the boundary conditions is
The version of equation which describes the supersymmetric variation of the action and includes the four fermi terms is
If we write the gravitino variation in the interior, then integration by parts adds a term to other boundary terms, where
A slight rearrangement gives
We see clearly the term which cancels the extrinsic curvature and a term involving the Yang-Mills supercurrent which partially cancels the variation of the Yang-Mills part of the action. The penultimate term cancels the variation of the supercurrent. The variation of the action under the supersymmetry transformations can be obtained by combining the boundary terms with terms from the variation of the matter multiplet and with terms which arise from the interior. The invariance of 11-dimensional supergravity ensures that the volume terms in the variation cancel. Boundary terms arise from the interior when partial integration has to be used. Our aim has been to vet whether heterotic M-theory on a flat background in its concrete low-energy formulation as Hoˇrava-Witten supergravity is stable. 11-dimensional supergravity on a manifold with boundary shows an amazing robustness. At each successive order in derivatives, the anomaly-free extension of the theory is very tightly constrained, but so far this has not forced any internal contradictions. This is consistent with the idea that the construction produces the low-energy limit of a well-defined theory of some kind. There may also be important implications for the allowed counterterms in quantised 11-dimensional supergravity, and it would be interesting to examine both interaction and counterterms on a manifold with boundary.
Heterotic Supergravity in D Dimensions
Starting from the bosonic field equations of the D-dimensional effective massless fully heterotic string which is the D-dimensional heterotic supergravity in this note we derive the first-order field equations by locally integrating the second-order field equations. By integration we mean cancelling an exterior derivative on both sides of the equations. Therefore we obtain a first-order formulation of the theory.
The reduction of the kinetic term for the 2-form potential yields the result
and the reduction of the Yang-Kinetic term gives
With these definitions at hand, the sum of the previous Lagrangians, the Einstein-Hilbert term and the kinetic terms for scalar fields produces the total d-dimensional bosonic Lagrangian
where the potential for the scalar fields is given by
With the definitions of the fermionic fields in d dimensions, their kinetic Lagrangian is completely diagonalized and takes the form
Next, we compute the supersymmetry transformation rules. A straightforward calculation yields for the bosons
Our results for the supersymmetry transformations of the fermionic fields are
In particular, the minimal coupling of gauge fields in the covariant derivative is given by
The effective action of low energy limit of heterotic string theory is
where
We have the multidimensional metric, the anti–symmetric Kalb-Ramond field, the dilaton and the set of U(1) gauge fields.
Collecting all the results we can now write down the D-dimensional Lagrangian
We have a new D-dimensional Lagrangian which yields the D-dimensional field equations and also the constraint
The gauge group is SO(1,1) in this case. The Lagrangian is
The Lagrangian for the theory in d dimensions is obtained by integrating the Lagrangian over the (D − d)-dimensional internal space. The dimensionally-reduced Lagrangian is therefore
where the Ricci scalar is
The resulting Lagrangian is
and the potential arises from the curvature of the internal space as
The action for a p-form potential is given by
The Hodge star operator for a p-form is defined as
It is generalised to (p,q)-forms on a Hermitian manifold (where D now denotes its complex dimension) by
This definition ensures that we have the following expression for the scalar product of two (p,q)-forms on a Hermitian manifold
In this work, by locally integrating the second-order field equations which are derived and which govern the massless sector of the D-dimensional fully heterotic string namely the D-dimensional heterotic supergravity we have obtained the first-order field equations of the theory which contain only a single exterior derivative acting on the potentials. When the field equations of the field strengths are substituted back in the Lagrangian one recovers the second-order formalism. In comparison with this scheme our first-order field equations of the D-dimensional heterotic supergravity do contain the basic fields except the graviton but on the contrary they do not include the field strengths. The first-order formulation of the D-dimensional heterotic supergravity presented in this note has two important implications. The first-order field equations play an important role in the coset construction of the supergravities. Thus as we have briefly discussed in the previous section the equations derived in this note can be considered to be essential ingredients of a possible coset construction of the heterotic supergravities. Secondly since the dual fields introduced in the first-order field equations can be arbitrarily varied one can make use of this fact to generate solutions. Therefore in this respect beside being first-order the integrated field equations containing parameters which can be manipulated become powerful tools in seeking solutions of the heterotic supergravities.
We have shown that there is a large class of solutions to the heterotic supergravity formulations. These theories are consistent in ten dimensions, in recent years it was discovered that all the consistent superstring theories are related to one another by dualities, namely S-duality and T-duality. This establishes type IIA and heterotic supergravity as limits of the same theory. T–duality relates both type II and both heterotic theories to each other, and S–duality relates type I to heterotic SO(32). We will provide a toy example that is consistent with the IIB supergravity equations of motion for RR and NS flux, their change under T–duality and the torsional relation for heterotic backgrounds. This implies a duality between heterotic string theory with NS5 branes and another heterotic theory with only flux. It would be intersting to find out what this means at the topological string level. Since there are no open heterotic strings, the interpretation as an open/closed duality fails. In this sense, the interpretation of the geometric transition we propose for heterotic strings is not as clear as that for type II theories. The symmetries of the supergravity theories have been studied in recent years to gain insight in the symmetries and the duality transformations of the superstring theories. Especially the global symmetries of the supergravities contribute to the knowledge of the non-perturbative U-duality symmetries of the superstring theories and the M theory. An appropriate restriction of the global symmetry group of the effective low energy limit supergravity theory to the integers is conjectured to be the U-duality symmetry of the relative superstring theory. Therefore, we claim these backgrounds are also transition duals. Supergravity equations of motion and the torsional constraint for heterotic strings pose severe restrictions on the allowed type of fluxes. We provide a toy example that is consistent with the IIB orientifold action, the IIB linearized supergravity equation of motion and the torsional relation in the U–dual heterotic background. These backgrounds come in pairs and we argued them to be related by a geometric transition, meaning that one of them contains branes, the other one only flux. A rigorous proof of this claim and the implications for weak–strong coupling dualities in the underlying field theories are left for future work. The supergeometrical origin of this theory is remarkable. Supergravitational theories can be constructed from any superfield representation of the super-Poincaré group as follows: Pick a superfield which contains a scalar at the component level. Construct an action from this field which is invariant under rigid scale transformations but which has the wrong sign kinetic term. Finally, gauge the rigid scale transformations. This will be a theory of supergravity with compensator. These results primarily provide an embedding of a large class of half-maximal gauged supergravities in heterotic supergravity, and hence in string theory. They also highlight the absence of such origins for some noncompact gauged supergravities that are of considerable interest in fewer than ten dimensions. This counting is far from a full treatment of the effective action or even the massless spectrum resulting from compactification on the geometry. First of all, one must include the new light modes arising from toroidal compactifications. After including these new fields, one way to get an upper bound on the number of massless fields would be to count the solutions of the variations of all the fermions that satisfy the linearized equations of motion. Unfortunately, these are complicated, coupled differential equations and perhaps no simpler to solve than other potential methods for addressing aspects of the effective action, such as trying to understand the moduli space of geometries. Reducing 11–dimensional supergravity on an interval one can obtain heterotic theory similarly as a weak coupling limit. At each end of the interval (whose length is proportional to the string coupling) there are spacetime filling planes with gauge group on them. One brane is usually called the hidden sector, the other one carries our observable world. The resulting description of supergravity is non-standard and, unfortunately, has not been worked out in any detail as of this writing. Further work in this direction has the potential to shed light on the relation to recent advances in our understanding of the heterotic supergravity. Nevertheless, even given the limitations of our computations, the results do have some interesting ranges of validity. It would be interesting to see whether these exceptional cases can be given a higher-dimensional interpretation by some other techniques. There are many technical issues raised by the above computations which should be solved and which moreover can be solved with presently available technology.








































































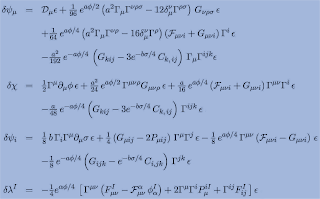











No comments:
Post a Comment