Type IIA supergravity is a ten-dimensional theory which can be obtained either by taking a certain limit in type IIA string theory, or by doing a dimensional reduction of eleven-dimensional supergravity, which is the supergravity theory with the highest possible dimensionality. The massless modes of a superstring can be described by an effective action which is the corresponding supergravity theory. Having mentioned that the type IIA supergravity action is obtained by a simple dimensional reduction from the eleven-dimensional theory would seem to indicate that this form of the theory is unique. Based on this conjecture, the 10D type IIA theory and all of its constituents should have their 11-dimensional origins. We would like to describe the interactions of the massless modes, which is constrained by supersymmetry to be described by the type IIA supergravity theory in ten dimensions. Type IIA supergravity is a ten-dimensional, non-chiral supergravity theory. A supergravity theory is a supersymmetric theory that includes gravity, the ten-dimensional metric is a bosonic field that enters the action. The fact that N = 2 means that the supersymmetry transformations of the fields are generated by two independent parameters. In ten dimensions, this means that the theory has 32 conserved supercharges. IIA supergravity is non-chiral, which means that the supersymmetry parameters have opposite chiralities. In components, type IIA supergravity describe the dynamics of the gravity supermultiplet. To make the local supersymmetry of this component formalism manifest, one proceeds as in global supersymmetry by introducing the notion of superspace and superfields. The massless bosonic field contents of type II can be divided in two sectors from its very first construction: the Neveu-Schwarz-Neveu-Schwarz sector (NSNS) and the Ramond-Ramond sector (RR). A well studied and unique example of a massive theory of gravity is the massive type IIA supergravity in ten dimensions constructed by Romans. Amongst massive theories, massive type IIA supergravities can be easily characterised solely by there field content in which the NSNS 2-rank tensor field is massive. Massive theories are continuous deformations of the regular ones in which the gauge transformations and supersymmetries get extra dependence via a mass parameter. Consequently, the equations of motion get extra terms linear and quadratic in this parameter.
Type IIA Supergravity
The type IIA supergravity in ten dimensions describes the low energy limit of type IIA superstrings. This theory is non-chiral and therefore it has no anomalies. We start by reviewing bosonic part of the standard IIA supergravity action. The 10D NSNS fields are the dilaton, 2-form potential and string frame metric. The 10D RR fieldstrenghts are the 4-form, 2-form and 0-form. The action is
The next step is the part of the 10D IIA supergravity action quadratic in fermions. We work in the string frame.
where the covariant derivatives act on the Majorana dilatino and gravitino are
The story for the 10D Type IIA supergravity action is similar. In the string frame this action is the sum of the Neveu-Schwarz, Ramond-Ramond and Chern-Simons sectors
where
The Einstein-frame action becomes
The action can be written as a total derivative using the form-field equations of motion
Massive IIA Supergravity
This section contains a review of Romans massive supergravity. Our starting point is the supersymmetric bosonic action of massive type IIA supergravity. In the language of differential forms, it is given by
For the form fields and dilaton, together with the Einstein equation
It is useful also to present the expressions for the ten-dimensional Hodge duals of the form fields. We find that they are given by
The action for massive type IIA supergravity in the Einstein frame reads
This action is a generalisation of the type IIA supergravity that is obtained from the low energy limit of type IIA string theory, although some care must be taken when taking the massless limit.
The terms in the ten-dimensional action which will contribute to the gravitino masses are
The equations of motion that follow from Lagrangian are
The gravitino and dilatino supersymmetry variations read
and
where the supercovariant derivative is given by
Duality–symmetric Type IIA D=10 Supergravity
We present different but classically equivalent forms of the action, give the analysis of symmetry and dynamical properties of the model, and establish the connection with the standard formulation of type IIA supergravity. We will focus on the subsector of ten–dimensional type IIA supergravity which does not involve the quartic fermion terms.
By use of the standard dimensional reduction procedure we get the following conventional part of the type IIA supergravity action
The complete action is
The reduction of this part of the action results in
To this end, as in the case of duality–symmetric D = 11 supergravity, it is convenient to rewrite the action as follows
with
The variation of this Lagrangian is
The dual field strengths are incorporated into the action
This action is the complete duality–symmetric action for type IIA supergravity up to the four–fermion terms and has the characteristic structure of duality–symmetric supergravities. To extend the action to the Romans’s massive supergravity let us continue with its bosonic sector in the form
The complete massive type IIA supergravity Lagrangian has the following form
This action is invariant under modified gauge transformations and local supersymmetry transformations
The duality-symmetric action for the massive type IIA supergravity has the following form
One can, modulo a total derivative, rewrite the Chern–Simons term such that

After that we arrive at the following action for N = 1, D = 10 supergravity
To summarize, we have constructed the duality–symmetric version of type IIA D = 10 supergravity which in its final form contains in addition to the standard type IIA supergravity bosonic fields also their duals. The coupling of this duality–symmetric type IIA supergravity to the Dp–branes and to the NS5–brane can be carried out in a conventional way.
We discussed earlier the massless contents of Type II supergravity theories. They naturally include graviton and at low energies they give supergravities as effective theories. In string theory, supergravities have their role as effective theories for describing the massless sector of the field theory limit to lowest order. As effective theories, the supergravity actions are expected to receive higher order derivative corrections. In the M-theory context in particular, there is very active research aimed at finding the correct modification of supergravity. The associated actions of type IIA strings are obtained by using the metrics and other background fields of the type IIA supergravities. The resulting actions agree with those of type IIA strings obtained in the study of the supergravities. Supersymmetry ensures that this theory is unique. Furthermore the IIA ten-dimensional supergravity has to be the dimensional reduction of the 11D higher-dimensional theory, since the two theories have the same supersymmetry algebras. The superfields which describe IIA D = 10 supergravity are subject to the constraints which are obtained from the D = 11 supergravity constraints using the ansatz and solving for Bianchi identities. One approach to deriving the exact supergravity solutions would be to work in the context of D = 11 supergravity. Since type IIA supergravity is related to eleven-dimensional supergravity by dimensional reduction, any exact solution of type IIA supergravity is related to a solution of D = 11 supergravity with translational invariance along one of the spatial directions. An interesting problem for future study is to construct the Lagrangian description of the consistent coupling of a type IIA supergravity action to an NS5-brane source. The latter requires the construction of a duality-symmetric version of type IIA supergravity by the dimensional reduction of the duality-symmetric D = 11 supergravity. The truncation of such a IIA supergravity action shall produce the duality-symmetric version of the N = 1, D = 10 supergravity, which should naturally couple to a heterotic fivebrane. Note that recent investigations of interacting brane actions may provide one with a possibility of making this coupling supersymmetric. Historically, eleven-dimensional supergravity theory is interesting because eleven is the highest dimension and supersymmetry invariance is possible. But one should keep in mind that, just as type IIA supergravity should only be seen as an effective theory at low energy but not a complete theory, the eleven-dimensional supergravity can only at best be a low-energy description of a consistent theory. It would be interesting to find other solutions of type IIA supergravity and to study their possible 11-dimensional origin. There are many potentially fruitful directions for future research.
Type IIA Supergravity
The type IIA supergravity in ten dimensions describes the low energy limit of type IIA superstrings. This theory is non-chiral and therefore it has no anomalies. We start by reviewing bosonic part of the standard IIA supergravity action. The 10D NSNS fields are the dilaton, 2-form potential and string frame metric. The 10D RR fieldstrenghts are the 4-form, 2-form and 0-form. The action is
The next step is the part of the 10D IIA supergravity action quadratic in fermions. We work in the string frame.
where the covariant derivatives act on the Majorana dilatino and gravitino are
The story for the 10D Type IIA supergravity action is similar. In the string frame this action is the sum of the Neveu-Schwarz, Ramond-Ramond and Chern-Simons sectors
where
The Einstein-frame action becomes
The action can be written as a total derivative using the form-field equations of motion
Massive IIA Supergravity
This section contains a review of Romans massive supergravity. Our starting point is the supersymmetric bosonic action of massive type IIA supergravity. In the language of differential forms, it is given by
For the form fields and dilaton, together with the Einstein equation
It is useful also to present the expressions for the ten-dimensional Hodge duals of the form fields. We find that they are given by
The action for massive type IIA supergravity in the Einstein frame reads
This action is a generalisation of the type IIA supergravity that is obtained from the low energy limit of type IIA string theory, although some care must be taken when taking the massless limit.
The terms in the ten-dimensional action which will contribute to the gravitino masses are
The equations of motion that follow from Lagrangian are
The gravitino and dilatino supersymmetry variations read
and
where the supercovariant derivative is given by
Duality–symmetric Type IIA D=10 Supergravity
We present different but classically equivalent forms of the action, give the analysis of symmetry and dynamical properties of the model, and establish the connection with the standard formulation of type IIA supergravity. We will focus on the subsector of ten–dimensional type IIA supergravity which does not involve the quartic fermion terms.
By use of the standard dimensional reduction procedure we get the following conventional part of the type IIA supergravity action
The complete action is
The reduction of this part of the action results in
To this end, as in the case of duality–symmetric D = 11 supergravity, it is convenient to rewrite the action as follows
with
The variation of this Lagrangian is
The dual field strengths are incorporated into the action
This action is the complete duality–symmetric action for type IIA supergravity up to the four–fermion terms and has the characteristic structure of duality–symmetric supergravities. To extend the action to the Romans’s massive supergravity let us continue with its bosonic sector in the form
The complete massive type IIA supergravity Lagrangian has the following form
This action is invariant under modified gauge transformations and local supersymmetry transformations
The duality-symmetric action for the massive type IIA supergravity has the following form
One can, modulo a total derivative, rewrite the Chern–Simons term such that
After that we arrive at the following action for N = 1, D = 10 supergravity
To summarize, we have constructed the duality–symmetric version of type IIA D = 10 supergravity which in its final form contains in addition to the standard type IIA supergravity bosonic fields also their duals. The coupling of this duality–symmetric type IIA supergravity to the Dp–branes and to the NS5–brane can be carried out in a conventional way.
We discussed earlier the massless contents of Type II supergravity theories. They naturally include graviton and at low energies they give supergravities as effective theories. In string theory, supergravities have their role as effective theories for describing the massless sector of the field theory limit to lowest order. As effective theories, the supergravity actions are expected to receive higher order derivative corrections. In the M-theory context in particular, there is very active research aimed at finding the correct modification of supergravity. The associated actions of type IIA strings are obtained by using the metrics and other background fields of the type IIA supergravities. The resulting actions agree with those of type IIA strings obtained in the study of the supergravities. Supersymmetry ensures that this theory is unique. Furthermore the IIA ten-dimensional supergravity has to be the dimensional reduction of the 11D higher-dimensional theory, since the two theories have the same supersymmetry algebras. The superfields which describe IIA D = 10 supergravity are subject to the constraints which are obtained from the D = 11 supergravity constraints using the ansatz and solving for Bianchi identities. One approach to deriving the exact supergravity solutions would be to work in the context of D = 11 supergravity. Since type IIA supergravity is related to eleven-dimensional supergravity by dimensional reduction, any exact solution of type IIA supergravity is related to a solution of D = 11 supergravity with translational invariance along one of the spatial directions. An interesting problem for future study is to construct the Lagrangian description of the consistent coupling of a type IIA supergravity action to an NS5-brane source. The latter requires the construction of a duality-symmetric version of type IIA supergravity by the dimensional reduction of the duality-symmetric D = 11 supergravity. The truncation of such a IIA supergravity action shall produce the duality-symmetric version of the N = 1, D = 10 supergravity, which should naturally couple to a heterotic fivebrane. Note that recent investigations of interacting brane actions may provide one with a possibility of making this coupling supersymmetric. Historically, eleven-dimensional supergravity theory is interesting because eleven is the highest dimension and supersymmetry invariance is possible. But one should keep in mind that, just as type IIA supergravity should only be seen as an effective theory at low energy but not a complete theory, the eleven-dimensional supergravity can only at best be a low-energy description of a consistent theory. It would be interesting to find other solutions of type IIA supergravity and to study their possible 11-dimensional origin. There are many potentially fruitful directions for future research.























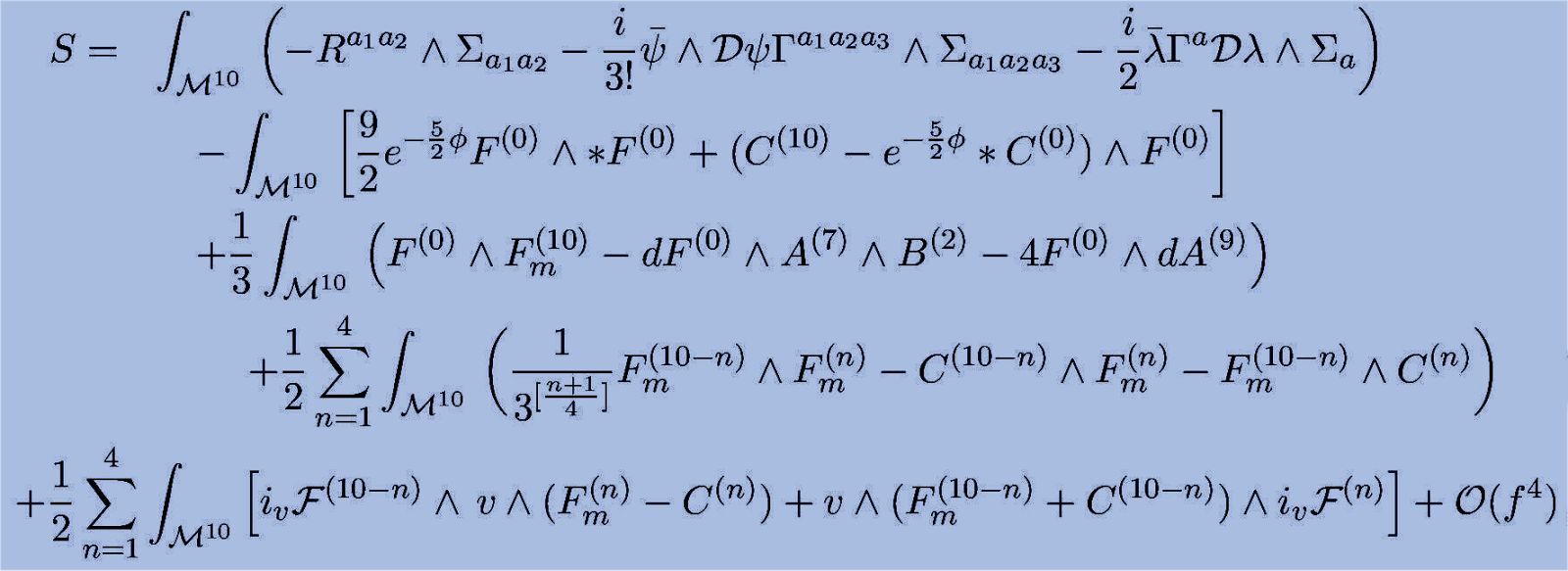

No comments:
Post a Comment