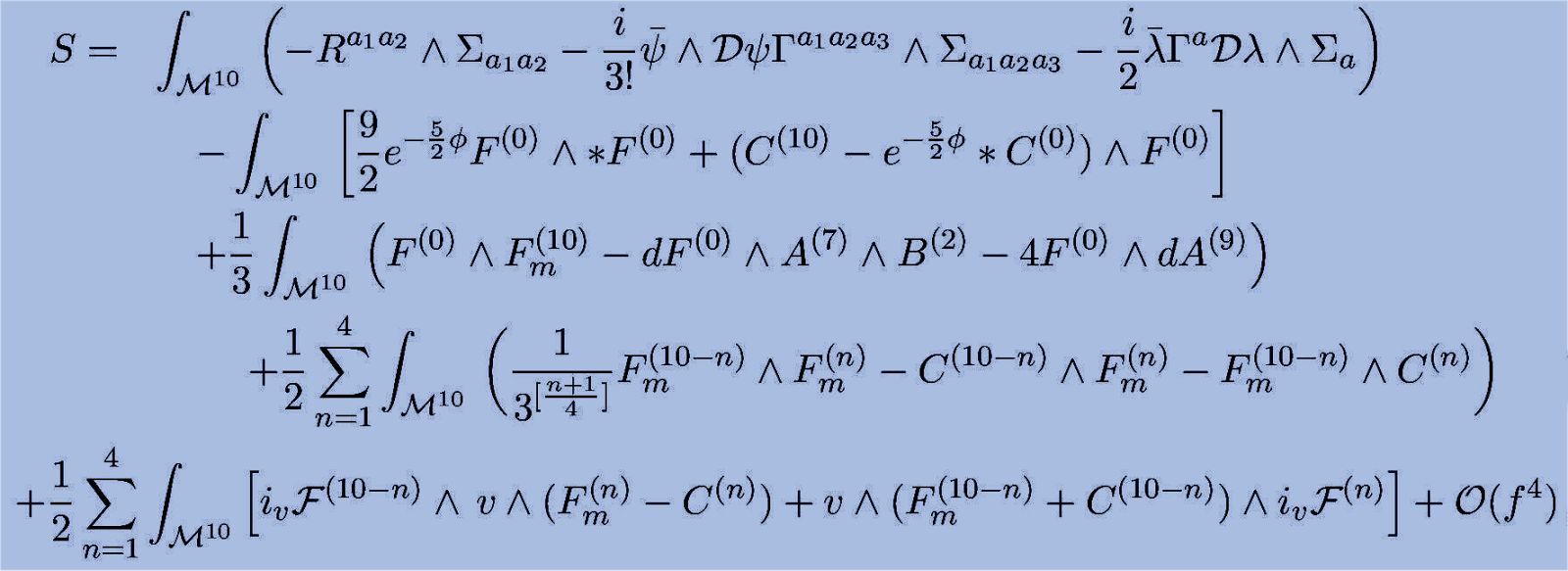Type IIB supergravity represents the low energy effective field theory describing massless particles with momenta below the scale of massive modes of the superstring. This is another maximal supergravity that can be constructed in ten dimensions. The type IIB theory is chiral and cannot be obtained by dimensional reduction from eleven dimensions. Nevertheless, it is related to type IIA supergravity by T-duality. Type IIB SUGRA contains, in addition to the generic fields of the Neveu-Schwarz (NS) sector, gauge potentials characteristic of the Ramond-Ramond (RR) sector. The bosonic fields of the IIB supergravity comprise of the graviton, the antisymmetric two form with a three-form field strength and the dilaton. The fermionic content of type IIB supergravity comprises a positive chirality dilatino and a negative chirality gravitino. Spinors in IIB are complex Weyl spinors. The gravitino and the dilatino have opposite chiralities, the supersymmetry parameter has the same chirality as the gravitino. Type IIB supergravity is the low-energy limit of type IIB string theory, which contains a fundamental string and various D-branes of odd D coupling to the gauge fields, similar to the even D-branes of type IIA. The action exhibits an interesting symmetry under modular transformations. Supersymmetry is used to derive conditions on higher derivative terms in the effective action of type IIB supergravity. Superstring effective actions are dependent on the actions of supergravity theories. Thus, there is much to be learned from the old techniques used to compactify them if we translate them to string language. The field equations and the supersymmetry transformations of type IIB supergravity can be worked out in a tricky manner. With the equations of motion identified, one looks at the supergravity action that reproduces these equations of motion and complements them with the self-duality condition. The dilaton and the axion are ordinary interacting particles in the low energy theory of superstring and thus should be treated on same footing as the other low energy fields such as the graviton, the antisymmetric second rank tensor and fermoins. Second, in a type IIB superstring or supergravity it is well known that the dilaton and the axion as well as the two 2-form antisymmetric tensor fields, those are, the NS-NS 2-form and the R-R 2-form, are doublets of the SL(2,R) Mobius group whereas the graviton and the 4-form gauge field are singlets in the Einstein metric. Thus, if we wish to show that they transform covariantly under the SL(2,R) transformation these local fields must be treated as not constants but fields. In this context, notice that the vanishing or constant dilaton and axion imply the vanishing 3-form field strengths, so in order to understand the transformation rules under the SL(2,R) we are led to consider the non-constant dilaton and axion. It was conjectured that type IIB theory in ten dimensions is endowed with SL(2,Z) symmetry. The discrete subgroup of the SL(2,R) group survives as an exact symmetry of the quantum theory and has been referred to as S-duality in the literature in analogy with the corresponding symmetry in heterotic string theory. There is mounting evidence for this symmetry and it has played a very important role in providing deeper insight into the nonperturbative attributes of type IIB theory.
Type IIB Supergravity
The bosonic field content of type IIB supergravity consists of the metric, two scalars, two 2-form potentials and a chiral 4-form potential with a self-dual 5-form field strength making up a total of 128 bosonic degrees of freedom. The fermionic field content consists of two Majorana–Weyl dilatini as well as two Majorana–Weyl gravitini comprising a total of 128 fermionic degrees of freedom. These fields are organized into one 10-dimensional N = 2 supergravity multiplet. The local supersymmetry algebra for this theory has been constructed and shown to only close on-shell.
The action of type IIB supergravity in the string frame is a sum of three terms
where
Modifed field strengths are used with
The starting point is the bosonic part of the Type IIB lagrangian density in 10D, which again involves the NS-NS fields and the Ramond-Ramond gauge potentials. The string-frame lagrangian for these fields is
To identify the on-shell action eliminate the Ricci scalar using the trace of the Einstein equations. Used in the action this yields
The on-shell action is
It is well-known that the covariant equations of motion for type IIB supergravity can not be derived from any action because of the presence of a self-dual five-form. However, after eliminating some unphysical fields, one arrives at equations of motion which are not manifestly covariant but admit a Lagrangian description. The formal covariance of the Lagrangian can then be provided by introducing auxiliary non-propagating fields. It is not possible to write a covariant action whose minimization gives the equations of motion 10-dimensional type IIB supergravity. The covariant action for type IIB supergravity can be written in the form
Decomposing this action up to the second order and omitting full-derivative terms, one obtains the quadratic action
The covariance of the action has to be taken with a grain of salt since one cannot impose any covariant gauge conditions on the auxiliary fields. Nevertheless, the very existence of the action allows one to study in detail the properties of supergravity. The existence of a covariant action for type IIB supergravity has special interest due to the discovery of the duality between type IIB superstring theory and the four-dimensional super Yang-Mills model.
Now we proceed with the gravitino field. The action for the gravitino field leading to the covariant equations of motion has the form
Taking into account that the gravitino field is left-handed
we rewrite the previous action as follows
The type IIB effective action at second order in derivatives may be written in non-linearly realised form with respect to the SL(2,Z) symmetry of the D = 10 type IIB theory. After expanding out the Cartan forms in the type IIB effective action at second order in derivatives is
Instead, we will use an action for the type IIB supergravity theory in ten dimensions that gives the correct equations of motion after imposing the self-duality condition as an additional constraint on these equations. This action, in string frame, takes the form
The type IIB low-energy effective action, in string frame, at second order in derivatives is
The five-form field strength self duality condition that must be imposed on the equations of motion that result from varying the type IIB action. Although not manifest in this formulation, type IIB supergravity possesses an SL(2,R) symmetry that is broken to an SL(2,Z) subgroup for the full type IIB string theory. Following the evidence, these theories have a huge group of global discrete symmetries. A particularly interesting subgroup is the SL(2,Z) S-duality of type IIB superstring theory which exchanges an infinite family of solitons and bound states. It was already known that the IIB supergravity, which is the low energy effective theory of the type IIB superstring theory, possesses a discrete global symmetry, the SL(2,R) symmetry, but this symmetry was regarded as an artifact of the low energy approximation to underlying renormalizable theory and not taken seriously in those days. But nowadays the situation has radically changed since the discovery of the still rather mysterious more fundamental theory where SL(2,Z) subgroup of SL(2,R) is expected to be an exact symmetry.
Dimensional Reduction of the Effective Action
We shall also need to consider the low-energy limit of the type IIB superstring for our discussion duality. The zero-slope limit of the type IIB superstring is given by N = 2, D = 10 chiral supergravity. This theory contains a metric, a complex antisymmetric tensor, a complex scalar and a four-index antisymmetric tensor gauge field. The compactifications of type IIA and type IIB theories as we go from ten to nine dimensions have been studied by Bergshoeff, Hull and Ortin and they have explored implications of various dualities for this compactification. More recently, Andrianopoli and collaborators have studied compactification of type II theories and M-theory in various dimensions. It is well known that type IIA and type IIB theories are related by T-duality below ten dimensions. In lower dimensions the S-duality combines with the T-duality leading to U-duality. Therefore, it is of interest to obtain type IIB effective action, through dimensional reduction, in lower dimensional spacetime and explore the implications of SL(2,R) duality transformations. Let us consider the ten dimensional action for the type IIB theory
In order to express the action in a manifestly SL(2,R) invariant form, recall that the axion and the dilaton parametrize the coset. We over to the Einstein frame through the conformal transformation and the previous action takes the form
The action is invariant under following transformations
The Einstein equation can be derived by varying the action with respect to the metric and the equation of motion associated with the antisymmetric tensor fields can be obtained in a straight forward manner.
The desired equation of motion, derived from the above action, is
Note that this is a matrix equation of motion and we have suppressed the indices for notational conveniences. It is worthwhile, at this stage to point out some similarities with the the global O(d,d) symmetry that arises when one considers toroidal compactifications to lower spacetime dimension.
We consider a string effective action in D spacetime dimensions with massless fields such as graviton, antisymmetric tensor, dilaton, and Abelian gauge fields. If we compactify coordinates on a d = D − 4 dimensional torus and assume that the backgrounds are independent of these d compact coordinates, the resulting four dimensional reduced effective action takes the following form
It is more convenient for the implementation of S-duality transformation to rescale the metric to Einstein metric, and introduce the axion. Then previous action can be expressed as
where
The equations of motion derived from the action are
and the Bianchi identity is
The S-duality transformations correspond to
where the metric and moduli remain invariant.
In summarizing, we have explored the consequences of S-duality transformations on the equations of motion with nonzero cosmological constant. First, we studied a four dimensional action in a general framework. The reduced action could have been obtained from toroidal compactification of a heterotic string effective action in higher dimensions. In this context, let us briefly discuss the presence of higher order terms and the consequences of the S-duality transformations in the equations of motion. We write down the next higher order term to the low energy string effective action as
We have checked that under the S-duality transformation with the additional term also breaks S-duality invariance. The graviton equation along with the higher order correction term as mentioned above is also not invariant under the S-duality. Thus it can be argued that the presence of the higher order terms do not restore the S-duality invariance in the equations of motion. Notice that when we dimensionally reduce the terms involving quadratic in curvature, there will be additional terms in involving moduli and gauge fields arising from dimensional reduction. We have seen that the contribution of previous action to equations of motion already breaks the S-duality. Therefore, even if we explicitly take into account the contribution coming from moduli and extra gauge fields in the corresponding equations of motion, the S-duality invariance will not be restored.
Higher Dimensional Effective Action
The purpose of this investigation is to study toroidal compactification of the type IIB theory and implications of SL(2,R) symmetry for the reduced action. It has been shown recently that the toroidally compactified type IIB string effective action possesses an SL(2,R) invariance as a consequence of the corresponding symmetry in ten dimensions when the self-dual five-form field strength is set to zero. The compactified theory on a d-dimensional torus respects the symmetry when we specify the transformation properties of the resulting scalar and vector fields. It is well-known that the equations of motion of type IIB supergravity theory can not be obtained from a covariant action because of the presence of a four-form gauge field with the self-dual field strength in the spectrum. This gauge field couples to a self-dual three-brane which can give rise to string solution.
The type IIB equations of motion can be derived from the following covariant action
The metric, the dilaton and the antisymmetric tensor represent the massless modes in the NS-NS sector of type IIB theory. Also the scalar and the antisymmetric tensor represent the massless modes in the R-R sector. The reduced action takes the form
The reduced action have an SL(2,R) invariance which can be better understood by rewriting the action in the Einstein frame. The metric in the Einstein frame is related with the string metric as given in the second section. The action in the Einstein frame takes the following form
If we define the following SL(2,R) matrix then the previous action can be expressed in the manifestly SL(2,R) invariant form as
The action is invariant under the following global SL(2,R) transformation
Finally, the tensor field strength, defined above, can be shown to be gauge invariant by defining appropriate gauge transformations
The D-dimensional effective action takes the following form
Recalling our convention, the action for a p-forms is reduced according to
With our simplifications, toroidal compactification of a supergravity theory from D to d dimensions, containing the universal NSNS sector and a p-form, leads to the d-dimensional Poincaré invariant action
In compactifications of field theories from D to d dimensions, we require to obtain a background with a maximally symmetric d-dimensional space-time, but without any assumption on the geometry of the internal space, as long as it is compact. This allows to change the background values of the internal components of gauge invariant fields, without affecting the space-time symmetry in d dimensions. It is evident from the D-dimensional action that dilaton and axion interact with antisymmetric tensor fields, gauge fields and the scalars due to the presence of matrix in various terms and these interaction terms respect the SL(2,R) symmetry. It is important know what type of dilatonic potential is admissible in the above action which respects the S-duality symmetry. We reach a surprizing conclusion that the presence of interaction terms of the form only adds constant term which amounts to adding cosmological constant term to the reduced action. Note that the Einstein metric is SL(2,R) invariant and one can add terms involving higher powers of curvature (higher derivatives of metric) to the action and maintain the symmetry. However, we are considering the case when the gravitational part of the action has the Einstein-Hilbert term only.
The reduction to IIB is achieved when the generalised metric is taken to be the fundamental object rather than the supergravity fields themselves. These only arise upon choosing a specific parameterisation. If one had viewed the supergravity fields as fundamental, one could not have obtained a reduction to IIB. This approach allows both type II theories to appear within the same duality manifest theory. Unlike its type IIA counterpart, the type IIB supergravity can not be obtained by dimensional reduction of 11D supergravity on a circle, namely, from the low energy limit of M-Theory. Nonetheless, a strong-coupling completion of certain type IIB supergravity theories in ten dimensions is known. It is referred to as F-Theory, is formulated in twelve dimensions and makes extensive use of the nonperturbative SL(2,Z) self-duality of type IIB superstring theory. F-theory provides a realisation of IIB as a reduction from a higher-dimensional theory. The extra dimensions geometrise the S-duality of IIB supergravity so that one has a twelve-dimensional theory. There were hints that this geometrisation could be extended to the U-dualities of type IIB. F-theory is expected to give a systematic description of the IIB superstring with non-trivial dilaton and axion background to which the complex structure of a two-dimensional torus would correspond. To explain the origin of the SL(2,Z) duality of the type IIB theory has been a main motivation of F theory. In this respect it may be interesting to examine whether the theory of SL(2,Z)-covariant super D3-brane may have a 12 dimensional interpretation. Finally, a study of general dilaton and axion may shed light on F-theory, a conjectured 12-dimensional quantum field theory underlying a type IIB superstring. F-theory is expected to give a systematic description of the IIB superstring with non-trivial dilaton and axion background to which the complex structure of a two-dimensional torus would correspond. The IIB case seems to have a much richer spectrum of solutions than the IIA case. Although these new solutions are also incomplete in the sense that the sources are smeared, they constitute an important step since they change the existing paradigm that tree-level scale separation is only possible in massive IIA. Besides providing more examples of tree-level scale separation, the examples in IIB could be relevant for improving our understanding of the subtleties in such backgrounds. The IIB supergravity theory is not known to have massive deformations. One of the reasons for this is that there is no candidate vector field like in the IIA case. This type II T –duality maps the symmetries of each individual ten-dimensional type II theory into the other. This is specially useful when one symmetry is manifest in one theory but not in the other. This is the case of SL(2,R), which is manifest in the type IIB theory but it is not manifest by any means in the type IIA theory. The type IIB supergravity in ten dimensions has an explicit SL(2,R) symmetry of the equations of motion which is broken to SL(2,Z) by quantum corrections. This is the conjectured SL(2,Z) S–duality discrete gauge symmetry of the type IIB string, while SL(2,R), which we shall also refer to as an S–duality, is a solution-generating symmetry, transforming any given solution into a new one. The level of low energy effective action that this SL(2,R) invariance of the type IIB theory survives the toroidal compactification. In fact, this is not surprising since a symmetry in a higher dimensional theory should become a part of the bigger symmetry in the lower dimensional theory, although in this case, it requires quite non-trivial calculation to prove the invariance. Hence it is enough for our purposes to calculate the coefficient in type IIB string theory. The reason we want to do the calculation in the type IIB theory is because we want to impose the constraints implied by S–duality which allow us to obtain explicit expressions for these amplitudes at high genera. The main output obtained by imposing the constraints of supersymmetry and S–duality for a certain class of interactions in the type IIB effective action is that the moduli dependent coefficients of these interactions satisfy first order differential equations on moduli space. This holds to all orders in the expansion. We shall simply write very schematically the structure of these equations which is good enough for our purposes. Based on the constraints of supersymmetry and S–duality of the type IIB theory, we are able to find at least a part of the coefficients of certain higher genus amplitudes which yield the transcendental nature of the term in the M theory effective action. Our work emphasizes the important role supersymmetry and U–dualities play in constraining the effective action in general. Learning about the symmetries of the ten-dimensional theory they descend from is then essential for a proper understanding of the lower dimensional theories. As we have mentioned, there are more string-like solutions not only with electric charge but also with magnetic charge in type II theories in lower dimensions which should form multiplets of bigger symmetry group, the U-duality group. Apart from the string-like solutions, there are also other p-brane solutions in these theories which deserve a systematic study to properly identify the complete U-duality group. This will provide strong evidence for the conjecture of the U-duality symmetries in those theories.
Type IIB Supergravity
The action of type IIB supergravity in the string frame is a sum of three terms
Modifed field strengths are used with
The starting point is the bosonic part of the Type IIB lagrangian density in 10D, which again involves the NS-NS fields and the Ramond-Ramond gauge potentials. The string-frame lagrangian for these fields is
To identify the on-shell action eliminate the Ricci scalar using the trace of the Einstein equations. Used in the action this yields
The on-shell action is
It is well-known that the covariant equations of motion for type IIB supergravity can not be derived from any action because of the presence of a self-dual five-form. However, after eliminating some unphysical fields, one arrives at equations of motion which are not manifestly covariant but admit a Lagrangian description. The formal covariance of the Lagrangian can then be provided by introducing auxiliary non-propagating fields. It is not possible to write a covariant action whose minimization gives the equations of motion 10-dimensional type IIB supergravity. The covariant action for type IIB supergravity can be written in the form
Decomposing this action up to the second order and omitting full-derivative terms, one obtains the quadratic action
The covariance of the action has to be taken with a grain of salt since one cannot impose any covariant gauge conditions on the auxiliary fields. Nevertheless, the very existence of the action allows one to study in detail the properties of supergravity. The existence of a covariant action for type IIB supergravity has special interest due to the discovery of the duality between type IIB superstring theory and the four-dimensional super Yang-Mills model.
Now we proceed with the gravitino field. The action for the gravitino field leading to the covariant equations of motion has the form
Taking into account that the gravitino field is left-handed
we rewrite the previous action as follows
The type IIB effective action at second order in derivatives may be written in non-linearly realised form with respect to the SL(2,Z) symmetry of the D = 10 type IIB theory. After expanding out the Cartan forms in the type IIB effective action at second order in derivatives is
Instead, we will use an action for the type IIB supergravity theory in ten dimensions that gives the correct equations of motion after imposing the self-duality condition as an additional constraint on these equations. This action, in string frame, takes the form
The type IIB low-energy effective action, in string frame, at second order in derivatives is
The five-form field strength self duality condition that must be imposed on the equations of motion that result from varying the type IIB action. Although not manifest in this formulation, type IIB supergravity possesses an SL(2,R) symmetry that is broken to an SL(2,Z) subgroup for the full type IIB string theory. Following the evidence, these theories have a huge group of global discrete symmetries. A particularly interesting subgroup is the SL(2,Z) S-duality of type IIB superstring theory which exchanges an infinite family of solitons and bound states. It was already known that the IIB supergravity, which is the low energy effective theory of the type IIB superstring theory, possesses a discrete global symmetry, the SL(2,R) symmetry, but this symmetry was regarded as an artifact of the low energy approximation to underlying renormalizable theory and not taken seriously in those days. But nowadays the situation has radically changed since the discovery of the still rather mysterious more fundamental theory where SL(2,Z) subgroup of SL(2,R) is expected to be an exact symmetry.
Dimensional Reduction of the Effective Action
We shall also need to consider the low-energy limit of the type IIB superstring for our discussion duality. The zero-slope limit of the type IIB superstring is given by N = 2, D = 10 chiral supergravity. This theory contains a metric, a complex antisymmetric tensor, a complex scalar and a four-index antisymmetric tensor gauge field. The compactifications of type IIA and type IIB theories as we go from ten to nine dimensions have been studied by Bergshoeff, Hull and Ortin and they have explored implications of various dualities for this compactification. More recently, Andrianopoli and collaborators have studied compactification of type II theories and M-theory in various dimensions. It is well known that type IIA and type IIB theories are related by T-duality below ten dimensions. In lower dimensions the S-duality combines with the T-duality leading to U-duality. Therefore, it is of interest to obtain type IIB effective action, through dimensional reduction, in lower dimensional spacetime and explore the implications of SL(2,R) duality transformations. Let us consider the ten dimensional action for the type IIB theory
In order to express the action in a manifestly SL(2,R) invariant form, recall that the axion and the dilaton parametrize the coset. We over to the Einstein frame through the conformal transformation and the previous action takes the form
The action is invariant under following transformations
The Einstein equation can be derived by varying the action with respect to the metric and the equation of motion associated with the antisymmetric tensor fields can be obtained in a straight forward manner.
The desired equation of motion, derived from the above action, is
Note that this is a matrix equation of motion and we have suppressed the indices for notational conveniences. It is worthwhile, at this stage to point out some similarities with the the global O(d,d) symmetry that arises when one considers toroidal compactifications to lower spacetime dimension.
We consider a string effective action in D spacetime dimensions with massless fields such as graviton, antisymmetric tensor, dilaton, and Abelian gauge fields. If we compactify coordinates on a d = D − 4 dimensional torus and assume that the backgrounds are independent of these d compact coordinates, the resulting four dimensional reduced effective action takes the following form
It is more convenient for the implementation of S-duality transformation to rescale the metric to Einstein metric, and introduce the axion. Then previous action can be expressed as
where
The equations of motion derived from the action are
and the Bianchi identity is
The S-duality transformations correspond to
where the metric and moduli remain invariant.
In summarizing, we have explored the consequences of S-duality transformations on the equations of motion with nonzero cosmological constant. First, we studied a four dimensional action in a general framework. The reduced action could have been obtained from toroidal compactification of a heterotic string effective action in higher dimensions. In this context, let us briefly discuss the presence of higher order terms and the consequences of the S-duality transformations in the equations of motion. We write down the next higher order term to the low energy string effective action as
We have checked that under the S-duality transformation with the additional term also breaks S-duality invariance. The graviton equation along with the higher order correction term as mentioned above is also not invariant under the S-duality. Thus it can be argued that the presence of the higher order terms do not restore the S-duality invariance in the equations of motion. Notice that when we dimensionally reduce the terms involving quadratic in curvature, there will be additional terms in involving moduli and gauge fields arising from dimensional reduction. We have seen that the contribution of previous action to equations of motion already breaks the S-duality. Therefore, even if we explicitly take into account the contribution coming from moduli and extra gauge fields in the corresponding equations of motion, the S-duality invariance will not be restored.
Higher Dimensional Effective Action
The purpose of this investigation is to study toroidal compactification of the type IIB theory and implications of SL(2,R) symmetry for the reduced action. It has been shown recently that the toroidally compactified type IIB string effective action possesses an SL(2,R) invariance as a consequence of the corresponding symmetry in ten dimensions when the self-dual five-form field strength is set to zero. The compactified theory on a d-dimensional torus respects the symmetry when we specify the transformation properties of the resulting scalar and vector fields. It is well-known that the equations of motion of type IIB supergravity theory can not be obtained from a covariant action because of the presence of a four-form gauge field with the self-dual field strength in the spectrum. This gauge field couples to a self-dual three-brane which can give rise to string solution.
The type IIB equations of motion can be derived from the following covariant action
The metric, the dilaton and the antisymmetric tensor represent the massless modes in the NS-NS sector of type IIB theory. Also the scalar and the antisymmetric tensor represent the massless modes in the R-R sector. The reduced action takes the form
The reduced action have an SL(2,R) invariance which can be better understood by rewriting the action in the Einstein frame. The metric in the Einstein frame is related with the string metric as given in the second section. The action in the Einstein frame takes the following form
If we define the following SL(2,R) matrix then the previous action can be expressed in the manifestly SL(2,R) invariant form as
The action is invariant under the following global SL(2,R) transformation
Finally, the tensor field strength, defined above, can be shown to be gauge invariant by defining appropriate gauge transformations
The D-dimensional effective action takes the following form
Recalling our convention, the action for a p-forms is reduced according to
With our simplifications, toroidal compactification of a supergravity theory from D to d dimensions, containing the universal NSNS sector and a p-form, leads to the d-dimensional Poincaré invariant action
In compactifications of field theories from D to d dimensions, we require to obtain a background with a maximally symmetric d-dimensional space-time, but without any assumption on the geometry of the internal space, as long as it is compact. This allows to change the background values of the internal components of gauge invariant fields, without affecting the space-time symmetry in d dimensions. It is evident from the D-dimensional action that dilaton and axion interact with antisymmetric tensor fields, gauge fields and the scalars due to the presence of matrix in various terms and these interaction terms respect the SL(2,R) symmetry. It is important know what type of dilatonic potential is admissible in the above action which respects the S-duality symmetry. We reach a surprizing conclusion that the presence of interaction terms of the form only adds constant term which amounts to adding cosmological constant term to the reduced action. Note that the Einstein metric is SL(2,R) invariant and one can add terms involving higher powers of curvature (higher derivatives of metric) to the action and maintain the symmetry. However, we are considering the case when the gravitational part of the action has the Einstein-Hilbert term only.
The reduction to IIB is achieved when the generalised metric is taken to be the fundamental object rather than the supergravity fields themselves. These only arise upon choosing a specific parameterisation. If one had viewed the supergravity fields as fundamental, one could not have obtained a reduction to IIB. This approach allows both type II theories to appear within the same duality manifest theory. Unlike its type IIA counterpart, the type IIB supergravity can not be obtained by dimensional reduction of 11D supergravity on a circle, namely, from the low energy limit of M-Theory. Nonetheless, a strong-coupling completion of certain type IIB supergravity theories in ten dimensions is known. It is referred to as F-Theory, is formulated in twelve dimensions and makes extensive use of the nonperturbative SL(2,Z) self-duality of type IIB superstring theory. F-theory provides a realisation of IIB as a reduction from a higher-dimensional theory. The extra dimensions geometrise the S-duality of IIB supergravity so that one has a twelve-dimensional theory. There were hints that this geometrisation could be extended to the U-dualities of type IIB. F-theory is expected to give a systematic description of the IIB superstring with non-trivial dilaton and axion background to which the complex structure of a two-dimensional torus would correspond. To explain the origin of the SL(2,Z) duality of the type IIB theory has been a main motivation of F theory. In this respect it may be interesting to examine whether the theory of SL(2,Z)-covariant super D3-brane may have a 12 dimensional interpretation. Finally, a study of general dilaton and axion may shed light on F-theory, a conjectured 12-dimensional quantum field theory underlying a type IIB superstring. F-theory is expected to give a systematic description of the IIB superstring with non-trivial dilaton and axion background to which the complex structure of a two-dimensional torus would correspond. The IIB case seems to have a much richer spectrum of solutions than the IIA case. Although these new solutions are also incomplete in the sense that the sources are smeared, they constitute an important step since they change the existing paradigm that tree-level scale separation is only possible in massive IIA. Besides providing more examples of tree-level scale separation, the examples in IIB could be relevant for improving our understanding of the subtleties in such backgrounds. The IIB supergravity theory is not known to have massive deformations. One of the reasons for this is that there is no candidate vector field like in the IIA case. This type II T –duality maps the symmetries of each individual ten-dimensional type II theory into the other. This is specially useful when one symmetry is manifest in one theory but not in the other. This is the case of SL(2,R), which is manifest in the type IIB theory but it is not manifest by any means in the type IIA theory. The type IIB supergravity in ten dimensions has an explicit SL(2,R) symmetry of the equations of motion which is broken to SL(2,Z) by quantum corrections. This is the conjectured SL(2,Z) S–duality discrete gauge symmetry of the type IIB string, while SL(2,R), which we shall also refer to as an S–duality, is a solution-generating symmetry, transforming any given solution into a new one. The level of low energy effective action that this SL(2,R) invariance of the type IIB theory survives the toroidal compactification. In fact, this is not surprising since a symmetry in a higher dimensional theory should become a part of the bigger symmetry in the lower dimensional theory, although in this case, it requires quite non-trivial calculation to prove the invariance. Hence it is enough for our purposes to calculate the coefficient in type IIB string theory. The reason we want to do the calculation in the type IIB theory is because we want to impose the constraints implied by S–duality which allow us to obtain explicit expressions for these amplitudes at high genera. The main output obtained by imposing the constraints of supersymmetry and S–duality for a certain class of interactions in the type IIB effective action is that the moduli dependent coefficients of these interactions satisfy first order differential equations on moduli space. This holds to all orders in the expansion. We shall simply write very schematically the structure of these equations which is good enough for our purposes. Based on the constraints of supersymmetry and S–duality of the type IIB theory, we are able to find at least a part of the coefficients of certain higher genus amplitudes which yield the transcendental nature of the term in the M theory effective action. Our work emphasizes the important role supersymmetry and U–dualities play in constraining the effective action in general. Learning about the symmetries of the ten-dimensional theory they descend from is then essential for a proper understanding of the lower dimensional theories. As we have mentioned, there are more string-like solutions not only with electric charge but also with magnetic charge in type II theories in lower dimensions which should form multiplets of bigger symmetry group, the U-duality group. Apart from the string-like solutions, there are also other p-brane solutions in these theories which deserve a systematic study to properly identify the complete U-duality group. This will provide strong evidence for the conjecture of the U-duality symmetries in those theories.